|
Ребус бр.159
Словни ребус
( 6 )

Решење: ДОАЈЕН ( до А је Н )
Пошто знамо да у решењу учествује и глагол БИТИ, лако долазимо до решења Иначе би морали да
утврдимо да преостлих четири слова (6 - 2), не представљју један већ два кључа
Ребус бр.160
Словни ребус
( 1,7,5,6 )
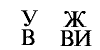
Решење: У НАСЛОВУ ВАЖНА ВИЈЕСТ ( У на слову В, а Ж на ВИ јест )
Претежак ребус у овом моменту, а и иначе тежак ребус. Главна потешкоћа је у откривању кључа СЛОВО
већ на самом почетку решавања А ту је још и кључ ЈЕСТ,глаголски обликкоји се ретко користи у
говорном језику. Овај пример уврстили смо и због принципа демократичности како би дали прилику
малоброним поборницима тврдње да су словни ребуси нерешиви! Решивост овог одличног ребуса могла би
да се знатно повећа добрим асоцијвтивним коментаром
Ребус бр.161
Словни ребус
( 8,6 )
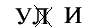
Решење: УПОРЕДНЕ ЛИНИЈЕ ( У поред не Л, И није )
Одличан и веома економичан ребус. Два кључа решења проистичу из узајамних односа слова, а
трећи је условљен графичким исказом У ребусу бр. 78, дато је опширнтје образложење за кључ НИЈЕ
које у потпуности важи и у овом случају.
Ребус бр.162
Диребус
( 3,6;4,6 )
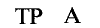
Решење: САТ РАНИЈЕ; СА МОЈЕ СТРАНЕ
До првог решења долазимо лако методом коу смо применили у претходном ребусу са Т Р,А није, па
уређена фраза даје - Сат раније. Околност да слово
А није са неким од слова ТР, односно да су САМО слова Т или Р једна СА другим омогућила је аутору
да у истој поставци пронађе и друго решење, дакле САМО је с Т Р, А НЕ - СА моје стране.Инпозантно, зар не!
Ребус бр.163
Словни ребус
( 6,6 )
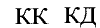
Решење: ПРЕКИД СУКОБА ( пре К и Д, су К оба )
Двословну групу са истим словима решавамо једним од могућих кључева пар, два или ОБА. Решење
друге групе могло би да гласи К и Д. Пошто је група КК, ПРЕ групе К и Л пишемо: Пре К и Д су К
оба. Увек када имате решење ребуса прочитајте га поново посматрајући притом његову поставку.
Меморисање тих мећузависности поставки и решења, помоћи ће вам да се лакше и тачније одлучите за
метод којом почињете решавање. Овај изванредан ребус са четири кључв И, СУ, ОБА, ПРЕ састанио је Момир Вученовић
|